Fathul Akbar

Volum Kubus

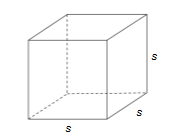
Perhatikan gambar kubus berikut ini.

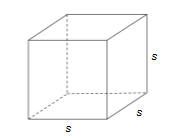
Volum sebuah kubus dengan rusuk s dapat ditentukan dengan rumus berikut ini :

Contoh :

Sebuah akuarium berbentuk kubus dengan panjang rusuk 30 cm. Berapa literkah air yang diperlukan untuk memenuhi akuarium tersebut?

Jawab :

Untuk menentukan banyaknya air yang dapat digunakan untuk memenuhi akuarium, kita harus menentukan volum dari akuarium tersebut.

Volum akuarium 
= volum kubus 
= s x s x s
= 30 x 30 x 30
= 9.000 cm3
= 9 dm3
= 9 liter

Volum Balok

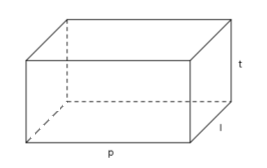
Perhatikan gambar balok berikut ini.

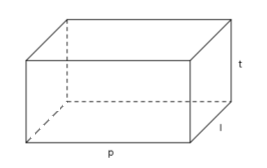
Volum sebuah balok dengan panjang p, lebar l, dan tinggi t dapat ditentukan menggunakan rumus sebagai berikut :

Contoh :

Pada permasalahan yang dihadapi oleh Andika, diketahui bahwa bak mandi di rumah Andika berbentuk balok dengan panjang 2 meter, lebar 1 meter, dan tinggi satu meter.

Volum bak mandi 
= volum balok
= p x l x t
= 2 x 1 x 1
= 2 m3
= 2.000 dm3
= 2.000 liter

Karena satu buah ember mampu menampung 10 liter air, maka untuk memenuhi bak mandi tersebut Andika harus mangangkut ember tersebut sebanyak = 2.000 : 10 = 200 kali.

Volum Prisma

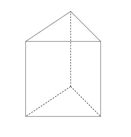
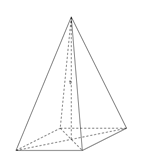
Perhatikan gambar prisma berikut ini.

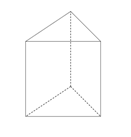
Gambar di atas merupakan salah satu contoh prisma yang disebut prisma segitiga.
Dinamakan demikian karena alasnya berbentuk bangun segitiga. Dengan kata lain, penamaan suatu prisma didasarkan pada bentuk alasnya.

Secara umum, volum suatu prisma tegak dapat ditentukan dengan menggunakan rumus sebagai berikut :

Contoh :

Sebuah prisma memiliki alas berbentuk segitiga siku-siku dengan alas 8 cm dan tinggi 6 cm. Jika tinggi prisma tersebut adalah 15 cm, berapakah volum prisma tersebut?

Jawab :

Luas alas prisma 
= ½ x 8 x 6
= 24 cm2

Vprisma 
= luas alas x tinggi
= 24 x 15 
= 360 cm3

Volum Limas

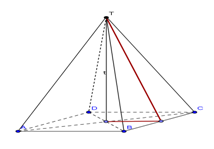
Perhatikan gambar berikut ini.

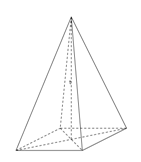
Gambar di atas merupakan salah satu contoh limas yang disebut limas segiempat.
Dinamakan demikian karena alasnya berbentuk bangun segiempat. Dengan demikian sama halnya dengan prisma, penamaan suatu limas didasarkan pada bentuk alasnya.

Secara umum, volum suatu limas dapat ditentukan dengan menggunakan rumus sebagai berikut :

Contoh :

Sebuah limas memiliki alas berbentuk belah ketupat dengan diagonal 12 cm dan 10 cm. Jika tinggi limas tersebut adalah 20 cm, berapakah volum limas tersebut?

Jawab :

Luas alas limas 
= Luas belah ketupat 
= ½ x d1 x d2 
= ½ x 12 x 10
= 60 cm2

Volum limas 
= 1/3 x luas alas x tinggi
= 1/3 x 60 x 20
= 400 cm3

Luas Permukaan Kubus

Perhatikan gambar kubus berikut ini.

Permukaan sebuah kubus terdiri atas 6 buah persegi yang kongruen, sehingga luas permukaan sebuah kubus sama dengan jumlah luas keenam persegi tersebut.

Mari kita selesaiakan permasalahan yang dihadapi oleh Rima

Pada permasalahan yang dihadapi oleh Rima,

Karena luas kertas kado kurang dari luas permukaan hadiah, berarti kertas kado tersebut tidak cukup untuk membungkus hadiah tersebut.

Dengan demikian, Rima harus membeli lebih dari satu kertas kado untuk dapat membungkus hadiah untuk adiknya.

Luas Permukaan Balok

Perhatikan gambar balok berikut ini.

Permukaan sebuah balok terdiri atas 6 buah persegi panjang, sehingga luas permukaan sebuah balok sama dengan jumlah luas keenam persegi panjang tersebut.

Contoh :

Sebuah kotak permen berbentuk balok berukuran panjang 10 cm, lebar 5 cm, dan tinggi 6 cm.

Luas permukaan kotak permen 
= (2 x p x l) + (2 x p x t) + (2 x l x t) 
= (2 x 10 x 5) + (2 x 10 x 6) + (2 x 5 x 6)
= 100 + 120 + 60
= 280 cm2

Luas Permukaan Prisma

Perhatikan gambar prisma berikut ini.

Gambar di atas merupakan salah satu contoh prisma yang disebut prisma segitiga. Dinamakan demikian karena alasnya berbentuk bangun segitiga. Dengan kata lain, penamaan suatu prisma didasarkan pada bentuk alasnya.

Permukaan prisma terdiri atas selimut, alas, dan tutup. Selimut sebuah prisma dapat berbentuk persegi atau persegi panjang, sedangkan alasnya berbentuk sama dengan tutupnya. Dengan demikian, menentukan luas permukaan sebuah prisma sama dengan menentukan jumlah luas selimut, luas alas, dan luas tutupnya.

Contoh :

Sebuah prisma memiliki alas berbentuk segitiga siku-siku dengan alas 8 cm dan tinggi 6 cm. Jika tinggi prisma tersebut adalah 15 cm, berapakah luas permukaan prisma tersebut?

Jawab :

Keliling alas = 8 + 6 + 10 = 24 cm.
Luas selimut prisma = Keliling alas x tinggi = 24 x 15 = 360 cm2.
Luas alas prisma = ½ x 8 x 6 = 24 cm2.

Luas permukaan prisma 
= Luas selimut + ( 2 x Luas alas )
= 360 + (2 x 24) 
= 360 + 48
= 408 cm2

Luas Permukaan Limas

Perhatikan gambar berikut ini.

Gambar di atas merupakan salah satu contoh limas yang disebut limas segiempat. Dinamakan demikian karena alasnya berbentuk bangun segiempat. Dengan kata lain, penamaan suatu limas didasarkan pada bentuk alasnya.

Permukaan limas terdiri atas sebuah alas dan sisi-sisi tegak. Sisi-sisi tegak suatu limas berbentuk segitiga. Dengan demikian, menentukan luas permukaan sebuah limas sama dengan menentukan jumlah luas sisi-sisi tegak dan luas alasnya.

Luas permukaan prisma = Luas alas + Luas sisi-sisi tegak.

Contoh :

Perhatikan gambar berikut.

Jika alas limas di atas berbentuk persegi dengan sisi 6 cm dan tinggi limas tersebut adalah 4 cm, Berapakah luas permukaan limas tersebut?

Jawab :

Luas alas limas = sisi x sisi = 6 cm x 6 cm = 36 cm2.

Luas sisi-sisi tegak = 4 x ( ½ x 6 x 5) = 60 cm2.

Luas permukaan limas 
= Luas alas + Luas sisi-sisi tegak 
= 36 cm2 + 60 cm2 
= 96 cm2